matlab对矩阵函数求导的方法教程

MATLAB对矩阵函数求导的方法教程

矩阵对矩阵求导的方法

在MATLAB中，对矩阵进行求导可以通过多种方法实现，主要包括使用雅可比矩阵和内置的diff函数。以下是详细的步骤和方法：

使用雅可比矩阵进行求导

• 程序示例： matlab v=[0.27,0.269993,0.269979,0.269957,0.269928,0.26989,0.269843,0.269786,0.26972,0.269643,0.269554,0.269454,0.26934,0.269213,0.269071,0.268914,0.268739,0.268547,0.268334,0.268101,0.267845,0.267564,0.267257,0.26692,0.266551,0.266...];
• 结果展示： 通过特定的程序计算，可以得到矩阵的导数。

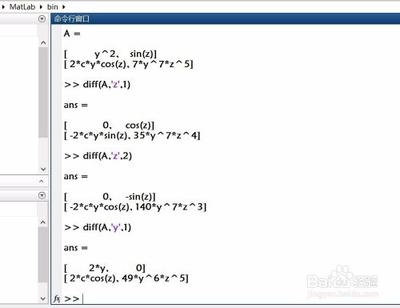
使用内置的diff函数

MATLAB内置了diff函数，用于对向量、矩阵甚至符号表达式进行一阶或高阶求导。例如，diff(f)可以计算函数f的一阶导数，而diff(f, n)则用于求n阶导数。

多项式及其表示

在MATLAB中，多项式通常用向量来表示。例如，多项式(P(x)=ax^2+bx+c)可以用向量p = [a, b, c]来表示。

数值微分方法

对于复杂的函数或者无法用符号表达式表示的情况，可以使用数值微分方法来近似求导。数值微分中的中点公式法是一种常用的方法。

实际应用示例

单变量函数的求导

以f(x)=sin(x)+x^2为例，在MATLAB中进行求导的操作步骤如下：

1. 声明符号变量x。
2. 定义函数f(x)。
3. 使用diff(f(x))计算一阶导数。
4. 使用pretty(ans)将结果转换为易读形式。

多元函数的求导

对于含有多个变量的函数，如f(x1, x2, x3)=sin(x1)+x2^2+exp(x3)，需要将每一个变量声明为符号变量，然后使用diff函数分别对每个变量求偏导数。

矩阵数据的求导及可视化

首先创建一个矩阵数据，然后使用diff函数对矩阵数据进行一阶求导，并使用绘图函数进行可视化展示。这种方法可以帮助我们直观地理解数据的趋势和变化。

通过上述方法，可以在MATLAB中对不同类型的函数和矩阵进行有效的求导操作，无论是简单的单变量函数还是复杂的多元函数，都能找到相应的解决方案。